The Derivative G of a Function G is Continuous and Has Exactly Two Zeros Selected Values
ofa function g iS continuous and has exactly two zeros. Selected values of g' are The derivative In the table above Ifthe domain of gis the set of all real numbers, then g is decreasing on which given of the following intervals? -2<152 only (B) ~ISISl only (C) X2-2 (D) 122 only (E) TS-2 0r ,2 2 The radius of a circle 1s increasing at & constant rate of 0 2 meters per second What iS the Fate of Increase In the area of the circle at the instant when the curcumference of the circle is 20R meters? 0.047m" /sec (B) 0Axm | sec (C) 4m" Jscc (DJ 203 m" / scc (EJ 1003m" Sec Let f bea differentiable function with f(2) =} &d f (2)=-5 and let gbe the function defined by g(x)=xf(r) Which of the following an equation of the line ungent t0 Ihe grph of gat the point whcte I =27 Je3x J-3=-5(-2) Y-6=-5(-2) Page

Related Question
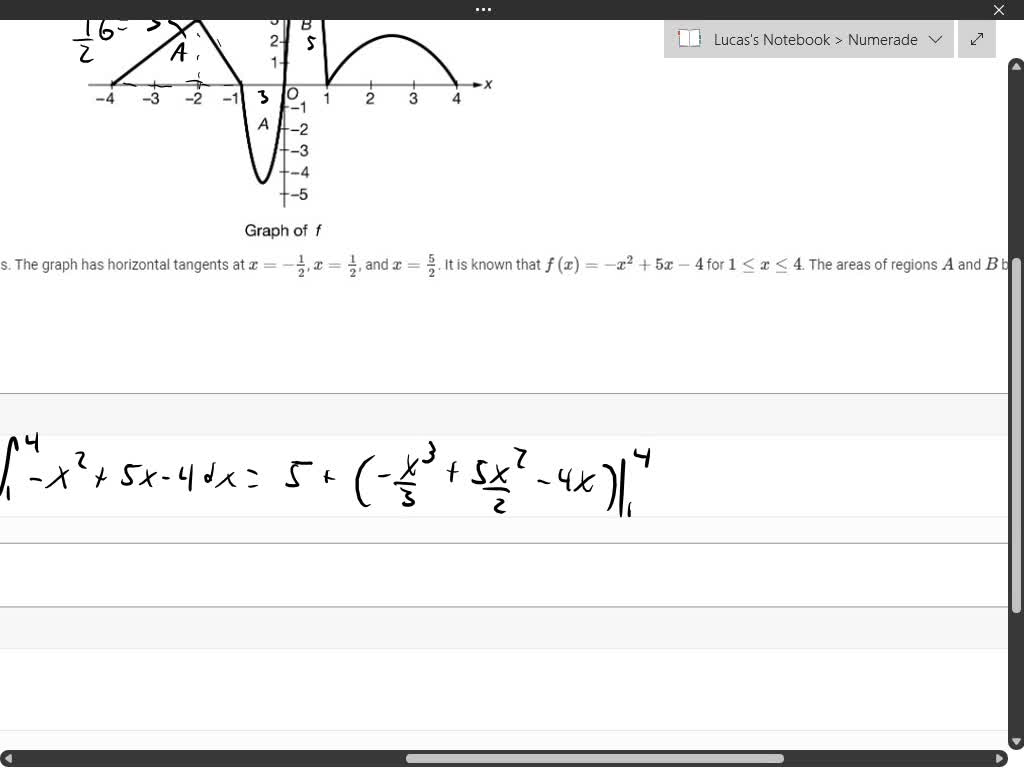
The continuous function f is defined for −4≤x≤4. The graph of f, shown above, consists of two line segments and portions of three parabolas. The graph has horizontal tangents at x=−12, x=12, and x=52. It is known that f(x)=−x2+5x−4 for 1≤x≤4. The areas of regions A and B bounded by the graph of f and the x-axis are 3 and 5, respectively. Let g be the function defined by g(x)=∫x−4f(t)ⅆt.
Discussion
You must be signed in to discuss.
Video Transcript
Okay. So here we have the graph of F. And we are told, let's see here define between negative and positive 42 line segments and portions of three. Parabolas horizontal tangents at X equals negative one half positive one half and 5/2. And we have that it is negative X squared plus five X minus four between one and four. That the areas of regions A and B bounded by the graph of F. And the X axis are three and five respectively. That's three, that's five. We are told to let G be the function defined by G of X equals the integral. From negative four up to acts of F. Of T. DT. So we would have G of zero. It's going to be equal to the integral from negative four up to zero of F F T DT. So let's see here. So from negative four is it from negative or? Yes it is. Okay. So First of all we can see that the area from -4 to negative one. This whole area can be calculated simply by using the equation for the area of a triangle. So it's one half base times height. You can see that the base is a width of three. Height is also three. So it would be one half of six equals three. That's our area for that region. Then we would subtract off the area of part A. So actually shouldn't no wow, do not do not know what just happened there. Okay, so that's the case. We can see that actually the it's the same amount of area being contained in those two regions. So that would actually mean that the integral from negative 4-0 of FTD. T simply going to be equal to zero. Additionally, because of the way that this is essentially sort of constructive, we're just adding on bits and pieces as we go along For finding GF four. We have that GF four is going to be equal to G of zero plus the integral from Oh actually that's not the easiest way of expressing this. Okay. Oh actually no I'll correct myself here. It would be equal to G of zero plus the integral from zero to positive four of F F T DT which Would be just zero plus that integral. and for finding the integral from 0-4. What we can do His first note that that would be encompassing that area B Which which that had a value of five. So it would be five plus the integral from 1 to 4 of. Let's see here, that's negative X squared plus five X minus four. That's five X minus four. Dx Would then be equal to five Plus negative x cubed over three Plus five x squared over two minus four X Evaluated from 1 to 4 will give us a final result here of Alright, so we will get a value of 19/2 when we evaluate that from end to end. Oh actually pardon me we would have 19/2 is the um Oh no no, never mind. Take that back. Yeah it's 19/2 then for B we are asked to find the absolute minimum value of G on the closed interval from negative four to positive four. And to justify our our answer. So we know that if we're looking for extreme A we want to differentiate our expression. So we have that D by dx of G of X going to be equal to D by D X. The integral from negative 42 X of F F T D T. Which is just going to equal G of X. Or not G of X but me just equal F of X. So we want to find when f of x equals zero. Have that f of x equals zero at -4 at negative one at zero at one and at four. But specifically if we have that F of X is the derivative of G of X. We want to look for if we're looking for absolute minimum where he wants to look for where we go from being negative to being positive. So where we've swapped from decreasing to increasing, you can see that that will occur at x equals zero. So we know that we want XP equal to zero. Which then in turn means that G of zero which we've already found G of zero equals zero is our absolute minimum value. Then we are asked to find all intervals on which the graph of G is concave down. Were asked to give a reason for our answer. Well, we would want to have the second derivative DVD X squared these weird by the X squared G of X would be equal to the derivative of F of X. So we want to find or if we're looking for where the graph of G is concave down, That would be equivalent to when f of four win the derivative of F of X Is less than zero. So that's negative second derivative. So he wants to look for where our function would be decreasing. So you can see that is occurring between negative two And Let's see that looks about to be about 0.5 there And from 0.5 to one. So actually I'll write these down here. We would have X in the interval from negative 22 as negative one half. Union with the interval from positive 1/2 up to or excuse me. Union with the interval. Oh yes, pardon me. Union with the interval from positive one half to one. Union with the interval from That looks to be about 2.5 up to four because those are the intervals where we can see that F of X is decreasing
Source: https://www.numerade.com/ask/question/ofa-function-g-is-continuous-and-has-exactly-two-zeros-selected-values-of-g-are-the-derivative-in-the-table-above-ifthe-domain-of-gis-the-set-of-all-real-numbers-then-g-is-decreasing-on-whic-61267/

Postar um comentário for "The Derivative G of a Function G is Continuous and Has Exactly Two Zeros Selected Values"